Question

HELP!!! What is the least common denominator of the expression below?

Answer 1

`\textsf{C.} \quad (x+6)(x-2)(x+1)`

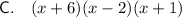
Explanation:

Given expression:

`(x^2+6)/(x^2+4x-12)+(7x)/(x^2+7x+6)`

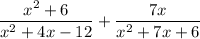
When adding and subtracting fractions, we must ensure that we have the same denominator. To do this, we usually multiply the two terms on the bottom to get the same denominator.

As the fractions are algebraic, first factor their denominators:

`\begin{aligned}x^2+4x-12 & = x^2 +6x-2x-12\\& = x(x+6)-2(x+6)\\& = (x-2)(x+6)\end{aligned}`

`\begin{aligned}x^2+7x+6 & = x^2 +6x+1x+6\\& = x(x+6)+1(x+6)\\& = (x+1)(x+6)\end{aligned}`

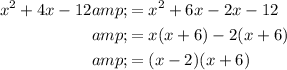
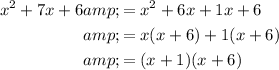
Therefore:

`\implies (x^2+6)/((x-2)(x+6))+(7x)/((x+1)(x+6))`

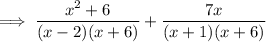
As the denominators of both fractions have a common factor of (x + 6), we only need to multiply the numerator and denominator of the left fraction by (x + 1) and the numerator and denominator of the right fraction by (x - 2) to get the same denominator.

Therefore, the common denominator is:

`(x+6)(x-2)(x+1)`

Answer 2

C. (x + 6)(x - 2)(x + 1)

Explanation:

• obviously, 2 and -6 are zeros for the trinomial x² + 4x - 12

(just plug in 2 or -6 into the expression and you’ll get zero)

Then

x² + 4x - 12 = (x - 2)(x + 6)

•• on the other hand,

1 - 7 + 6 = 0 ⇒ -1 and -6 are the zeros of the trinomial x² + 7x + 6

Then

x² + 7x + 6 = (x + 1)(x + 6)

Conclusion:

The least common denominator of the whole expression is :

(x - 2)(x + 1)(x + 6)