Question

A sample of 2,500 people was asked how many cups of coffee they drink in the morning. You are given the following sample information. Cups of Coffee Frequency 0 700 1 900 2 600 3 300 2,500 Refer to Exhibit 5-7. The variance of the number of cups of coffee is _____.

Answer 1

Answer: V(X) = 0.96

Explanation: Variance is defined as the average of the squared difference from the sample or population mean.

For a discrete frequency distribution is calculated following the steps:

1) Determine expected value or mean:

`E(X)=(\Sigma xf)/(\Sigma f)`

`E(X)=(0(700)+1(900)+2(600)+3(300))/(2500)`

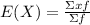
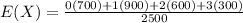
E(X) = 1.2

2) Multiply frequency and the squared difference of x and expected value:

`f(x-E(X))^(2)`

`700(0-1.2)^(2)=1008\\900(1-1.2)^(2) = 36\\600(2-1.2)^(2) = 384\\300(3-1.2)^(2) = 972`

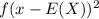
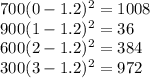
3) Add them:

`\Sigma [f(x-E(X))^(2)]` = 1008 + 36 + 384 + 972 = 2400

4) Divide the sum per frequency total:

`V(X)=(\Sigma [f(x-E(X))^(2)])/(\Sigma f)`

`V(X)=(2400)/(2500)`

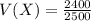
V(X) = 0.96

The variance of the number of cups of coffee is 0.96.