Question

Find a vector equation and parametric equations for the line segment that joins P to Q. P(1, −1, 4), Q(4, 2, 1)

Answer 1

( 1 + 3t, - 1 + 3t, 4 - 3t )

Explanation:

Hope this helps

Answer 2

Explanation:

Given points P(1, -1, 4), Q (4,2,1) vector equation of a line joining the points with position vectors r₀ and r₁ is:

r = (1 - t)r₀ + tr₁

where

t ∈ [0, 1]

and r₀ = P = (1, -1, 4)

r₁ = Q = (4, 2, 1)

r(t) = (1 - t)
`\langle 1,-1,4\rangle` + t
`\langle 4,2,1 \rangle`

`r(t) = \langle 1 - t , -1 + t, 4 - 4t \rangle + \langle 4t, 2t, t \rangle`

`r(t) = \langle 1 - t+4t , -1 + t+ 2t, 4 - 4t+ t \rangle`

`r(t) = \langle 1 +3t , -1 +3t, 4 - 3t \rangle`

∴

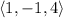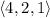
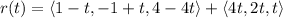
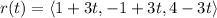
The vector equation
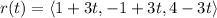`r(t) = \langle 1 +3t , -1 +3t, 4 - 3t \rangle` where t ∈ [0,1] is:

r(t) = (1+3t)i - (1+3t)j + (4 - 3t)k

The parametric equation is:

x(t) = 1 + 3t

y(t) = -1 + 3t

z(t) = 4 - 3t

(x(t), y(t), z(t) ) = ( 1 + 3t, -1 + 3t, 4 - 3t )