Answer:
The 90% confidence interval would be narrower than a 95% confidence interval
Explanation:
From the question we are told that
The 95% confidence interval is 0.69 to 0.91.
Generally the width of a confidence interval is dependent on the margin of error
Generally the margin of error is mathematically represented as
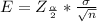
Here we see that
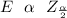
Here
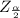 is the critical value of half of the level of significance .
is the critical value of half of the level of significance .
This value increase as the value of confidence level increase and vise versa
So for 90% confidence interval , the confidence level is 90% , hence the value of
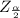 will decrease which will in turn decrease the value of E , hence the width of the interval will reduce
will decrease which will in turn decrease the value of E , hence the width of the interval will reduce
So the 90% confidence interval is narrower than a 95% confidence interval when the sample proportion or sample mean is constant