Question

A rectangular plot of farmland will be bounded on one side by a river and on the other three sides by a single-strand electric fence. With 1500 m of wire at your disposal, what is the largest area you can enclose, and what are its dimensions

Answer 1

Explanation:

Let x be the length and y be the width of the rectangular plot.

The plot is bounded on one side by a river and on the other three sides by a single-strand electric fence. It means,

x+2y = 1500

x = 1500 - 2y ....(1)

We know that the area of a rectangular plot is given by :

A = xy ....(2)

Put the value of x from equation (1) in (2)

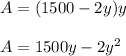`A=(1500-2y)y\\\\A=1500y-2y^2` .....(3)

For largest area, differentiate above area equation wrt y.

`(dA)/(dy)=(d)/(dy)(1500y-2y^2)\\\\=1500-4y\\\\\text{Put}\ (dA)/(dy)=0\\\\1500-4y=0\\\\y=(1500)/(4)\\\\=375`

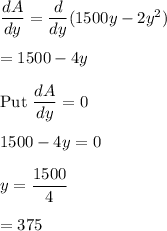
Put the value of y in equation (1).

x = 1500-2(375)

= 750 m

Put the value of y in equation (3).

`A =1500(375)-2(375)^2\\A=281250\ m^2`

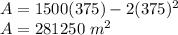
Hence, the largest area is 281250 m² and its dimensions are 750 m and 375 m.