Question

The tablet below represents ordered pairs that satisfy the functions f(x) and g(x). If f(x)=4x, which statements are true of g(x)? Select two options

Answer 1

By looking at the table, we can see that the value for g(x) is always f(x)-1. Thus we can conclude that

`g(x) = 4^x-1`

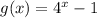
Now, think about the graph. For every value of y in f(x), the value of y in g(x) will be reduced by one. This means that the graph is translated down 1 unit!

The domain of both functions is actualy the same, that is,
`x\in\mathbb{R}`.

However, the range won't be the same. As
`x` approaches negative infinity, the exponentials always approaches zero. Thus, f(x) has range between zero and positive infinity. But, for g(x), we are subtracting one unit from the Y values, therefore the range will be between negative one and positive infinity. In conclusion, their range is different.

Overral: The true statements are the second and the fourth only

Answer 2

B and D are the correct answers.