We can find the value of x by solving the equation.
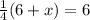 This is the given equation. Solve for x and we get the answer.
This is the given equation. Solve for x and we get the answer.
First, we distribute 1/4 in 6+x.
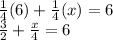
Because we have the denominators here, we have to get rid of them by multiplying whole equation by the highest denominator value.
The highest denominator value is 4, so multiply all whole equation by 4.
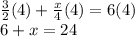
Then we move 6 to subtract on another side for the x to be the subject.
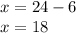
Therefore, the answer is x = 18.