Question

Multiply the polynomials show steps

Answer 1

3
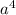`a^(4)` + 11a³ - 7a² + 18a - 18

Explanation:

When multiplying with two brackets, you need to multiply the three terms, (a²), (4a) and (-6) from the first bracket to all the terms in the second brackets, (3a²), (-a) and (3) individually. I have put each multiplied term in a bracket so it is easier.

(a² + 4a - 6) × (3a² - a + 3) =

(a² × 3a²) + {a² × (-a)} + (a² × 3) + (4a × 3a²) + {4a × (-a)} + (4a × 3) + {(-6) × a²) + {(-6) × (-a)} + {(-6) × 3}

Now we can evaluate the terms in the brackets.

(a² × 3a²) + {a² × (-a)} + (a² × 3) + (4a × 3a²) + {4a × (-a)} + (4a × 3) + {(-6) × a²) + {(-6) × (-a)} + {(-6) × 3} =

3
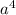`a^(4)` + (-a³) + 3a² + 12a³ + (-4a²) + 12a + (-6a²) + 6a + (-18)

We can open the brackets now. One plus and one minus makes a minus.

3
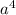`a^(4)` + (-a³) + 3a² + 12a³ + (-4a²) + 12a + (-6a²) + 6a + (-18) =

3
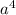`a^(4)` -a³ + 3a² + 12a³ -4a² + 12a -6a² + 6a -18

Evaluate like terms.

3
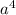`a^(4)` -a³ + 3a² + 12a³ -4a² + 12a -6a² + 6a -18 = 3
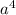`a^(4)` + 11a³ - 7a² + 18a - 18