Given:
The point is (8,5).
To find:
A point on the y-axis such that its distance from the point (8,5) is 10 units.
Solution:
Let the required point on the y-axis be (0,k).
Distance formula:
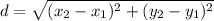
The distance between (8,5) and (0,k) is 10 units. Using distance formula, we get
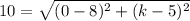
Taking square on both sides.
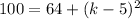
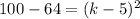
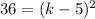
Taking square root on both sides.
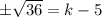
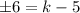
Now,
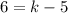 and
and
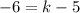
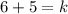 and
and
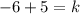
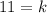 and
and
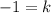
Therefore, the required point is either (0,11) or (0,-1).