Question

What is the solution to this system of equations?

10x-y=53
-13xt92
y=-----------------
2

Answer 1

x = 6, y = -113

Explanation:

10x - y = 53 --- Equation 1

y =
`(-13x+92)/(2)` --- Equation 2

I will be using the substitution method.

Substitute y =
`(-13x+92)/(2)` into Equation 1:

10x - y = 53

10x - (
`(-13x+92)/(2)`) = 53

I want to make the denominators on the left side of the equation the same, so I will multiply 10x by 2 so that I can get a fraction.

`(20x)/(2)` - (
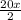`(-13x+92)/(2)`) = 53

Now that their denominators are both 2, I can combine the numerators under the same denominator.

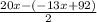`(20x-(-13x+92))/(2)` = 53

Two minuses, one outside a bracket and one inside makes a plus. One plus and one minus make a minus.

`(20x+13x-92)/(2)` = 53

Evaluate like terms.

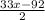`(33x-92)/(2)` = 53

Shift the (÷2) over to the right side and turn into (×2).

33x - 92 = 53 × 2

= 106

Shift the (-92) over to the right side and turn into (+92).

33x = 106 + 92

= 198

Find x.

x = 198 ÷ 33

x = 6

Substitute x = 6 into Equation 1:

10x - y = 53

10(-6) - y = 53

Evaluate.

-60 - y = 53

Shift the (-60) over to the right side and turn into (+60).

-y = 53 + 60

= 113

Find y.

y = -113