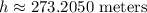Question

The angles of depression of two ships from the top of the light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the lighthouse.

please answer with figure.

​

Answer 1

273 meters

Step-by-step explanation:

See image attached for the diagram I used to represent this scenario.

The distance between the ships, at angles 30 and 45, is 200 meters. The distance between the left ship and the lighthouse is x meters.

We can use trigonometric ratios to solve this problem. We can use the tangent ratio
`\big{(} \frac{\text{opposite}}{\text{adjacent}} \big{)}` to create an equation with the two angles.

• 
  `\displaystyle \text{tan(45)} = (h)/(x)`
• 
  `\displaystyle \text{tan(30)} = (h)/(x+200) }`

Let's take these two equations and solve for x in both of them.

`\textbf{Equation I}`

• 
  `\displaystyle \text{tan(45)} = (h)/(x)`

tan(45) = 1, so we can rewrite this equation.

• 
  `\displaystyle 1=(h)/(x)`

Multiply x to both sides of the equation.

• 
  `\displaystyle x = h`

`\textbf{Equation II}`

• 
  `\displaystyle \text{tan(30)} = (h)/(x+200) }`

Multiply x + 200 to both sides and divide h by tan(30).

• 
  `\displaystyle \text{x + 200} = \frac{h}{\text{tan (30)}}`

Subtract 200 from both sides of the equation.

• 
  `\displaystyle \text{x} = \frac{h}{\text{tan (30)}} - 200`

Simplify h/tan(30).

• 
  `x=√(3)h - 200`

`\textbf{Equation I = Equation II}`

Take Equation I and Equation II and set them equal to each other.

• 
  `h=√(3)h-200`

Subtract √3 h from both sides of the equation.

• 
  `h-√(3)h=-200`

Factor h from the left side of the equation.

• 
  `h(1-√(3)) =-200`

Divide both sides of the equation by 1 - √3.

• 
  `\displaystyle h=(-200)/(1-√(3) )`

Rationalize the denominator by multiplying the numerator and denominator by the conjugate.

• 
  `\displaystyle h=(-200)/(1-√(3) ) \big{(} (1+√(3) )/(1+√(3)) \big{)}`
• 
  `\displaystyle h=(-200+200√(3) )/(1-3)`
• 
  `\displaystyle h =(-200+200√(3) )/(-2)`

Simplify this equation.

• 
  `\displaystyle h=100+100√(3)`
• 
  `h=273.20508075`

The height of the lighthouse is about 273 meters.

Answer 2

`h\approx 273.21 \text{ meters}`

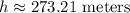
Explanation:

Please refer to the attachment.

In the attachment, h is the height of the lighthouse and x is the distance from the lighthouse to Ship A.

Since the angle of depression from the top of the lighthouse to Ship A is 45°, this means that the angle of elevation from Ship A to the top of the lighthouse is 45°.

Likewise, the angle of elevation from Ship B to the top of the lighthouse is 30°.

So, we will form two right triangles: the smaller, 45-45-90 triangle, and the larger 30-60-90 triangle.

Remember that in 45-45-90 triangles, the two legs are congruent.

Therefore, we can write that:

`h=x`

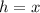
Next, in 30-60-90 triangles, the longer leg is always √3 times the shorter leg.

In our 30-60-90 triangle, the shorter leg is given by:

`\text{Shorter leg}=h`

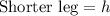
And the longer leg is given by:

`\text{Longer leg}=x+200`

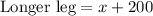
So, the relationship between the shorter leg and longer leg is:

`\sqrt3h = (x+200)`

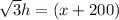
And since we know that h is equivalent to x, we can write:

`\sqrt3h=(h+200)`

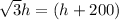
Now, we just have to solve for h. We can subtract h from both sides:

`\sqrt3h-h=200`

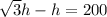
Factoring out the h yields:

`h(\sqrt3-1)=200`

Therefore:

`\displaystyle h=(200)/(\sqrt3-1)`

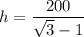
Approximate. So, the height of the lighthouse is approximately:

`h \approx 273.2050 \text{ meters}`