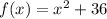Answer:
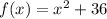
Explanation:
We want to find the equation in standard form for a polynomial that has zeros at x=6i and x=-6i.
So, we will have the two factors:
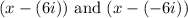
So, our polynomial will be:
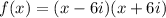
Distribute:
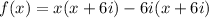
Distribute:

Combine like terms:
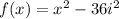
Remember that i²=-1. Hence:
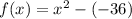
Simplify. So, our polynomial is: