Question

Help please! Figure ABCD is a rectangle. Find the
value of x.

Answer 1

⠀⠀⠀⠀⠀⠀☆☞Diagram☜☆

⠀⠀⠀⠀

`\setlength{\unitlength}{1 cm}\begin{picture}(20,15)\thicklines\qbezier(1,1)(1,1)(6,1)\qbezier(1,1)(1,1)(1,4)\qbezier(1,4)(1,4)(6,4)\qbezier(6,1)(6,1)(6,4)\qbezier(6,4)(6,4)(1,1)\qbezier(1,4)(1,4)(6,1)\put(0.7,0.5){\sf A}\put(6,0.5){\sf D}\put(1.4,4.3){\sf B}\put(6.6,4.3){\sf C}\put(3.4,2){\sf E}\put(1.5,2){\sf x + 11}\put(4.75,3){\sf 6x+1} {\boxed{\bold{X = ??}}}\end{picture}`

⠀⠀⠀⠀

______________________________

⠀⠀⠀⠀

AnswEr :

⠀⠀⠀⠀

• The value of x is 2

⠀⠀⠀⠀

━━━━━━━━━━━━━━━━━

⠀⠀⠀⠀

⠀⠀⠀⠀

➤ How to solve ?

⠀⠀⠀⠀

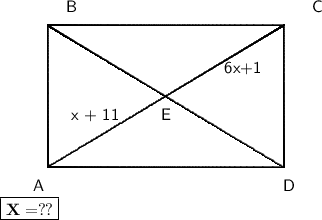
For solving such problems we need to recall some rules and properties of quadrilateral .

Above given figure is a figure of an rectangle . We know that the diagonals of an rectangle bisect each other

⠀⠀⠀⠀

Bisect is refer to dividing the line into 2 equal parts .

⠀⠀⠀⠀

From this property of the rectangle ; we can observe in the given rectangle that

⠀⠀⠀⠀

⠀⠀⠀⠀⠀⠀⠀⠀AE = EC

⠀⠀⠀⠀

━━━━━━━━━━━━━━━━━

⠀⠀⠀⠀

Solution :

⠀⠀⠀⠀

As , AE = EC

⠀⠀⠀⠀

➠ x + 11 = 6x + 1

⠀⠀⠀⠀

➠ x - 6x = 1 - 11

⠀⠀⠀⠀

➠ -5x = - 10

⠀⠀⠀⠀

➠ 5x = 10

⠀⠀⠀⠀

➠ x = 10/5

⠀⠀⠀⠀

➠ x = 2

⠀⠀⠀⠀

∴ The value of x is 2 .

━━━━━━━━━━━━━━━━━

Answer 2

Hello!

`\large\boxed{x = 2}`

As the figure is a rectangle, AE ≅ EC.

AE = x + 11

EC = 6x + 1

Set the two equal to each other:

x + 11 = 6x + 1

Subtract x from both sides:

11 = 5x + 1

Subtract 1 from both sides:

10 = 5x

Divide both sides by 5:

10/5 = 5x/5

x = 2.