Answer:
Test statistic
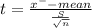
t = 1.076
Explanation:
Step(i):-
Given Mean of the Population (μ) = 8.0
Mean of the sample (x⁻) = 8.25
Given data
8,9,9,8,8,9,8,7
Given sample size n= 8
Given sample standard deviation(S) = 0.661
Step(ii):-
Null hypothesis : H: (μ) = 8.0
Alternative Hypothesis :H:(μ) > 8.0
Degrees of freedom = n-1 = 8-1=7
Test statistic
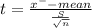
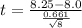
t = 1.076
Critical value
t₍₇,₀.₀₅₎ = 2.3646
The calculated value t = 1.076 < 2.3646 at 0.05 level of significance
Null hypothesis is accepted
Test the hypothesis that the true mean quiz score is 8.0 against the alternative that it is not greater than 8.0