Question

PLEASE HELP

Lester hopes to earn $1000 in interest in 3.3 years time from $10,000 that he has available to invest. To decide if it's feasible to do this by investing in an account that compounds annually, he needs to determine the annual interest rate such an account would have to offer for him to meet his goal. What would the annual rate of interest have to be? Round to two decimal places.

Answer 1

`r\approx0.03\text{ or about $3\%$}`

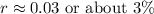
Explanation:

The standard compound interest formula is given by:

`\displaystyle A=P(1+(r)/(n))^(nt)`

Where A is the amount afterwards, P is the principal, r is the rate, n is the times compounded per year, and t is the number of years.

Since we are compounding annually, n=1. Therefore:

`\displaystyle A = P (1+r)^(t)`

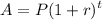
Lester wants to invest $10,000. So, P=10,000.

He wants to earn $1000 interest. Therefore, our final amount should be 11000. So, A=11000.

And our timeframe is 3.3 years. So, t=3.3. Substituting these values, we get:

`11000=10000(1+r)^(3.3)`

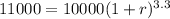
Let’s solve for our rate r.

Divide both sides by 10000:

`1.1=(1+r)^(3.3)`

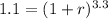
We can raise both sides to 1/3.3. So:

`\displaystyle (1.1)^(1)/(3.3)=((1+r)^(3.3))^(1)/(3.3)`

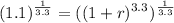
The right side will cancel:

`\displaystyle r+1=(1.1)^(1)/(3.3)`

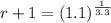
So:

`\displaystyle r=(1.1)^(1)/(3.3)-1`

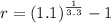
Use a calculator:

`r\approx0.03`

So, the annual rate of interest needs to be about 0.03 or 3% in order for Lester to earn his interest.