Question

The gravitational force of attraction be-

tween two students sitting at their desks in
physics class is 3.47 x 10-8 N.
If one student has a mass of 44.8 kg and the other has a mass of 53.9 kg, how far apart are the students sitting? The universal gravitational constant is 6.673 x 10 11 N m² kg?.
Answer in units of m.

please help!! :)

Answer 1

2.15 m

Step-by-step explanation:

Newton's Law of Universal Gravitation:

`\displaystyle F_g = G (m_1 m_2)/(r^2)`

• 
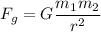
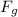  `\displaystyle F_g` is the gravitational force of attraction

• 
  `\displaystyle G` is the universal gravitational constant

• 
  `m_1` and
  `m_2` are the two masses of the two objects

• 
  `\displaystyle r` is the distance between the centers of the two objects.

List the known values:

• 
  `\displaystyle F_g = 3.47 \cdot 10^-^8 \ \text{N}`
• 
  `\displaystyle G = 6.673 \cdot 10^-^1^1 \ (Nm^2)/(kg^2)`
• 
  `\displaystyle m_1 = 44.8 \ \text{kg} \\ m_2 = 53.9 \ \text{kg}`
• 
  `\displaystyle r =\ ?`

Plug these values into the equation:

• 
  `\displaystyle 3.47 \cdot 10^-^8 \ \text{N} = 6.673 \cdot 10^-^1^1 \ (Nm^2)/(kg^2) \frac{(44.8 \ \text{kg})(53.9 \ \text{kg})}{r^2}`

Notice that the units
`\displaystyle \text{N}`,
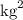`\displaystyle \text{kg}^2`, and
`\displaystyle \text{m}` cancel out. We are left with the unit
`\displaystyle \text{m}` for radius r.

Get rid of the units to make the problem easier to read.

• 
  `\displaystyle 3.47 \cdot 10^-^8= 6.673 \cdot 10^-^1^1 \ ((44.8)(53.9) \ )/(r^2)`

Multiply the masses together.

• 
  `\displaystyle 3.47 \cdot 10^-^8= 6.673 \cdot 10^-^1^1 \ ((2414.72))/(r^2)`

Multiply the gravitational constant and the masses together.

• 
  `\displaystyle 3.47 \cdot 10^-^8= (1.61134265\cdot 10^-^7)/(r^2)`

Solve for
`r^2` by dividing both sides by 3.47 * 10^(-8) and moving
`r^2` to the left.

• 
  `\displaystyle r^2 = (1.61134265\cdot 10^-^7)/(3.47\cdot 10^-^8)`
• 
  `r^2 = 4.64363876`

Take the square root of both sides.

• 
  `r=2.154910383`

The students are sitting about 2.15 m apart from each other.