4x² + 6x = 12
We move all the terms to the left:
- a = 4; b = 6; c = -12;
- Δ = b² - 4ac
- Δ = 6² - 4 · 4 · ( -12 )
- Δ = 228
The value of Δ is greater than zero, so the equation has two solutions
We use the following formulas to compute our solutions:
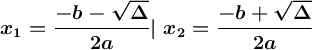
The end solution:
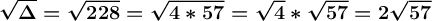
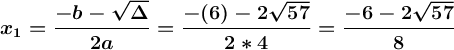
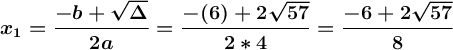
{ Pisces04 }