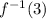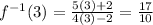Hello!
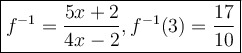
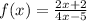
Find the inverse by swapping the x and y variables:
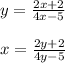
Begin simplifying. Multiply both sides by 4y - 5:
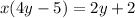
Start isolating for y by subtracting 2 from both sides:
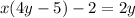
Distribute x:
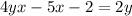
Move the term involving y (4yx) over to the other side:

Factor out y and divide:
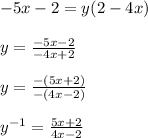
Use this equation to evaluate