Question

Find the limit.


`\large{lim_(x→5) \: \frac{ {x}^(2) - 5 }{ {x}^(2) + x - 30} }`


​

Answer 1

`\displaystyle \sf\lim_(x \to5)( \frac{ {x}^(2) - 5 }{ {x}^(2) + x - 30 } )`

Since the function is undefined for 5, evaluate the left-hand and right-hand limits

`\displaystyle \sf\lim_{x \to {5}^( - ) }( \frac{ {x}^(2) - 5 }{ {x}^(2) + x - 30 } ) \\\displaystyle \sf\lim_{x \to {5}^( + ) }( \frac{ {x}^(2) - 5 }{ {x}^(2) + x - 30 } )`

Evaluate the limit

`\sf - \infin \\ + \infin`

Since the left-hand and the right-hand limits are different, the limit does not exist

Answer 2

DNE (Doesn’t exist)

Explanation:

Hi! We are given the limit expression:

`\displaystyle \large{ \lim_(x \to 5) (x^2-5)/(x^2+x-30)}`

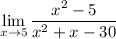
First step of evaluating limit is always directly substitution - substitute x = 5 in the expression.

`\displaystyle \large{ \lim_(x\to 5)(5^2-5)/(5^2+5-30)}\\ \displaystyle \large{ \lim_(x\to 5)(25-5)/(25+5-30)}\\ \displaystyle \large{ \lim_(x\to 5)(20)/(0)}`

Looks like we’ve got 20/0 after direct substitution. Note that this isn’t an indeterminate form but undefined since it’s not 0/0 which would make things different.

Now, plot the graph and see at x approaches 5, the function y approaches both positive infinity and negative infinity.

Introducing, left limit would be:

`\displaystyle \large{ \lim_(x \to 5^(-)) (x^2-5)/(x^2+x-30) = -\infty}`

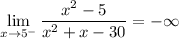
And right limit is:

`\displaystyle \large{ \lim_(x \to 5^(+)) (x^2-5)/(x^2+x-30) = \infty}`

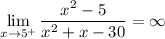
In limit, if both left and right limit are not equal then the limit does not exist.

From left limit and right, both are not equal. Therefore, the limit does not exist.

Cautions:

• Limit being DNE in this case simply means both left and right limit are not equal.
• The limit does not approach infinity a left limit apporoaches negative infinity as well which is different from positive infinity hence limit being DNE.