Question

Please answer both questions math

Answer 1

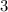`3` and perpendicular

Explanation:

It's important to remember that equations of lines are always set up in the format of
`y=mx+c`.

`y` is the
`y` value,
`m` is the gradient/slope,
`x` is the
`x` value and
`c` is the y-intercept.

Therefore, we must always rearrange our line equations so that
`y` is the subject.

In the first question, we are given the equation
`2x+6y=12`.

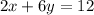We rearrange to make
`y` the subject:

`6y = 12-2x`

Then, we divide both sides by 6 to have the
`y` isolated:

`(6)/(6) y = (12)/(6) - (2)/(6)x\\\\ y = 2 - (1)/(3)x`

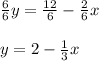
To find a perpendicular slope, we use the negative reciprocal of the original slope. The negative part of that means we negate the value (it becomes inverse) and the reciprocal part means that we flip the fraction.

So here, the slope is
`-(1)/(3)`.

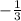So, the negative reciprocal of that would be
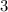`3` because we inverse the sign (the negative becomes positive) and the fraction is flipped to create
`(3)/(1)=3`.

So, the perpendicular slope is
`3`.

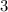In the second question, we have two equations. They both need to be rearranged to isolate the
`y`.

`4x-y=5\\4x = 5 + y\\y = 4x - 5\\\\4y = -x-12\\y = -(1)/(4)x - 3`

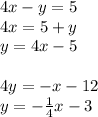
Look at the slopes of the two equations. If you look carefully, you will see that they are inverse of each other (one is positive and one is negative) and if you imagine
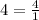`4 = (4)/(1)`, the fraction is flipped.

This means that the values are negative reciprocals of each other, meaning the lines are perpendicular.