Answer:
C
Explanation:
We have the system of equations:
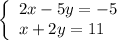
And an ordered pair (10, 5).
In order for an ordered pair to satisfy any system of equations, the ordered pair must satisfy both equations.
So, we can eliminate choices A and B. Satisfying only one of the equations does not satisfy the system of equations.
Let’s test the ordered pair. Substituting the values into the first equation, we acquire:
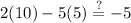
Evaluate:
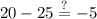
Evaluate:
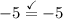
So, our ordered pair satisfies the first equation.
Now, we must test it for the second equation. Substituting gives:
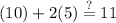
Evaluate:
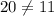
So, the ordered pair does not satisfy the second equation.
Since it does not satisfy both of the equations, the ordered pair is not a solution to the system because it makes at least one of the equations false.
Therefore, our answer is C.