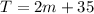Question

Sklyer heated up a bowl of “holiday punch” at a constant rate. After 5 minutes of heating, the punch was 45° F. After 18 minutes of heating, the punch was 71° F.

Write a linear equation to model this situation. Use T for Temperature and m for minutes heating.

Answer 1

`T=2m+35`

Explanation:

We know that after five minutes of heating, the punch was 45F.

And after 18 minutes of heating, the punch was 71F.

So, for our linear equation, we have two points: (5, 45) and (18, 71).

Using the two points, we can find the slope (in this case, the slope is the rate at which the temperature is increasing per minute).

The slope formula is given by:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

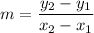
Let (5, 45) be (x₁, y₁) and let (18, 71) be (x₂, y₂). Substitute appropriately:

`\displaystyle m=(71-45)/(18-5)`

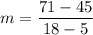
Evaluate:

`\displaystyle m=(26)/(13)=2`

So, the rate of heating is 2F per minute.

However, we still need to determine the original temperature of the punch. We can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

So, let’s substitute 2 for m and (5, 45) for our point. This yields:

`y-45=2(x-5)`

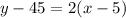
Distribute:

`y-45=2x-10`

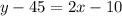
Add 45 to both sides. Therefore:

`y=2x+35`

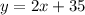
Since in this case, our dependent variable y is our temperature, we can replace it with T.

And our independent variable x is the minutes, we can replace it with m.

So, our equation is:

`T=2m+35`