We want to choose 4 people and we have 6 people to choose from. This is a combination of 6, 4 by 4. Also called six choose four.
The following formula:
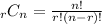
Is the combination of
 objects choosen from a total of
objects choosen from a total of
 . It's
. It's
 choose
choose
 .
.
For our problem, we just need to compute the following:
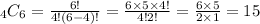
Thus
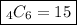
Therefore the answer is 15 different combinations