Question

Determine the measure of each segment then indicate whether the statements are true or false

Answer 1

`d_(AB)\\e d_(JK)`

`d_(AB)\\e \:d_(GH)`

`d_(GH)\\e \:d_(JK)`

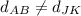
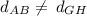
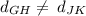
Therefore,

Option (A) is false

Option (B) is false

Option (C) is false

Explanation:

Considering the graph

Given the vertices of the segment AB

• A(-4, 4)

• B(2, 5)

Finding the length of AB using the formula

`d_(AB)\:=\:√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

`=√(\left(2-\left(-4\right)\right)^2+\left(5-4\right)^2)`

`=√(\left(2+4\right)^2+\left(5-4\right)^2)`

`=√(6^2+1)`

`=√(36+1)`

`=√(37)`

`d_(AB)\:=√(37)`

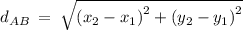
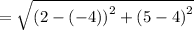
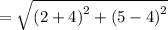
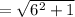
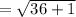
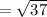
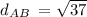
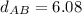`d_(AB)=6.08` units

Given the vertices of the segment JK

• J(2, 2)

• K(7, 2)

From the graph, it is clear that the length of JK = 5 units

so

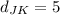`d_(JK)=5` units

Given the vertices of the segment GH

• G(-5, -2)

• H(-2, -2)

Finding the length of GH using the formula

`d_(GH)\:=\:√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

`=√(\left(-2-\left(-5\right)\right)^2+\left(-2-\left(-2\right)\right)^2)`

`=√(\left(5-2\right)^2+\left(2-2\right)^2)`

`=√(3^2+0)`

`=√(3^2)`

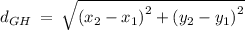
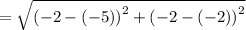
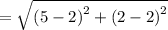
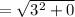
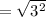
`\mathrm{Apply\:radical\:rule\:}\sqrt[n]{a^n}=a,\:\quad \mathrm{\:assuming\:}a\ge 0`

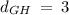`d_(GH)\:=\:3` units

Thus, from the calculations, it is clear that:

`d_(AB)=6.08`

`d_(JK)=5`

`d_(GH)\:=\:3`

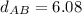
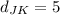
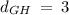
Thus,

`d_(AB)\\e d_(JK)`

`d_(AB)\\e \:d_(GH)`

`d_(GH)\\e \:d_(JK)`

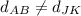
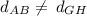
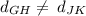
Therefore,

Option (A) is false

Option (B) is false

Option (C) is false