Question

Simplify. What are the restrictions on the variable? (2x/x-3)+(6/3-x)

Answer 1

V = 2

x ≠ 3

Explanation:

Simplifying

We are given the expression:

`\displaystyle V=(2x)/(x-3)+(6)/(3-x)`

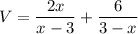
To simplify, we make both denominators equal by multiplying the second term by -1:

`\displaystyle V=(2x)/(x-3)-(6)/(x-3)`

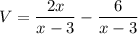
Now both denominators are equal, we simply add the numerators:

`\displaystyle V=(2x-6)/(x-3)`

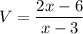
Factoring the numerator:

`\displaystyle V=(2(x-3))/(x-3)`

This expression can be simplified by x-3, but we must take into consideration the x-3 cannot be zero because it would cause an indetermination to appear.

The restriction is:

x - 3 ≠ 0

Or, equivalently:

x ≠ 3

Simplifying:

V = 2