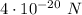Answer:
The gravitational force between the two planets is
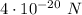
Step-by-step explanation:
Newton’s Law of Universal Gravitation
Objects attract each other with a force that is proportional to their masses and inversely proportional to the square of the distance between them.

Where:
m1 = mass of object 1
m2 = mass of object 2
r = distance between the objects' center of masses
G = gravitational constant:

The mass of the planets are:
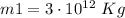
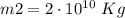
And the distance is:

Applying the formula:
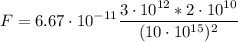
Calculating:
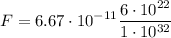
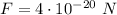
The gravitational force between the two planets is