Question

Plz help me im struggling hard​

Answer 1

Note that the cost for the rent is a function of the amount of the miles you drove. Let's call that
`C(m)`.

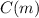Also note that the amount you pay will linearly increase, in other words, the increase in cost will always be the same for each mile. This tells us that our function is indeed a line, a first order polynomial of the form
`C(m) = am+b`

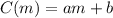
What would happen if you were to rent a truck and not drive it at all? You would pay only the one-time fee.

Therefore,
`C(0)=55`

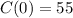
So,
`C(m) = am + 50`

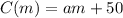
The cost will increase by $0.20 for each mile, wich tells us that
`a=0.20`

Finally, our expression is
`\boxed{C(m) = 0.2m+55}`

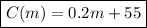
If we want to know how much would you pay if you drove 65 miles, we want to know what
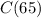`C(65)` is.

By plugging
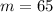`m=65` in the expression, we get

`C(65) =68`

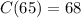
So you would pay $68

Answer 2

0.20 × 65 is what you would do for the second

Explanation:

btw listen to yungblud