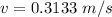Question

Suppose a clay model of a koala bear has a mass of 0.235 kg and slides on ice at a speed of 0.720 m/s. It runs into another clay model, which is initially motionless and has a mass of 0.305 kg. Both being soft clay, they naturally stick together. What is their final velocity (in m/s)

Answer 1

The value is
`v = 0.3133 \ m/s`

Step-by-step explanation:

From the question we are told that

The mass of the first model is
`m_1 = 0.235 \ kg`

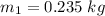
The sliding speed is
`u_1 = 0.720 \ m/s`

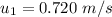
The mass of the second model is
`m_2 = 0.305 \ kg`

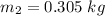
Generally from the law of momentum conservation w have that

`m_1 * u_1 + m_2 * m_2 * u_2 = (m_1 + m_2 ) v`

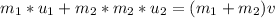
Here
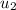`u_2` is the velocity of the second model and given that it is motionless at it initial state the value will be
`u_2 = 0 \ m/ s`

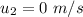
So

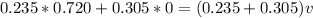
`0.235 * 0.720 + 0.305 * 0 = (0.235 + 0.305 ) v`

=>
`v = 0.3133 \ m/s`