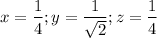Solution :
Let x, y, z be the dimensions of the rectangle.
Volume of the rectangle (V) = xyz
Given that the vertex should lie on ellipse
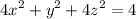 .......(i)
.......(i)
So here the volume xyz must be maximum with constraints above.
We solve this using Lagranches method with variable λ
Lagranches function is
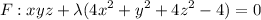 .....(ii)
.....(ii)
To find λ,
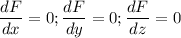
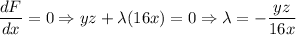 .............(iii)
.............(iii)
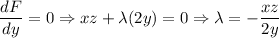 ..................(iv)
..................(iv)
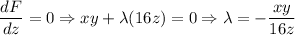 ...............(v)
...............(v)
Equating (iii) and (iv)
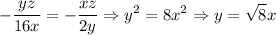 ...............(vi)
...............(vi)
Equating (iii) and (v)
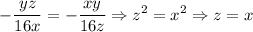 ....................(vii)
....................(vii)
Substitute (vi) and (vii) in (i),
From (i),
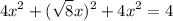
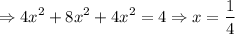
From (vi),
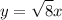
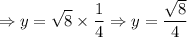
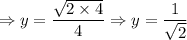
From (vii),
z = x
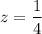
Therefore, for maximum volume the dimensions of a rectangle box are