Question

Let tk be the number of ways to choose k beads from a drawer that contains 10 red beads, 8 blue beads, and 11 green beads. Find the generating function for the sequence {tk} 29 k = 0. Do not find a formula for tk.

Answer 1

`\mathbf{G(x) = (1 + x)^(29)}`

Explanation:

From the given information;

The total number of beads = 10 + 8 + 11 = 29

To choose k beads out 29 beads, let assume that
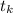`t_k` be the no. such that:

`t_k = ( ^(29)_(k)) \ \ \ where; k =0,1,2,3,....,29`

∴

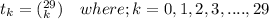
The sequence
`\{ t_k\}^(29)_(k=0) = (^(29)_(k))`

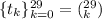
The generating function for
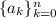`\{ a_k \}^n_(k=0)` is:

`G(x) = a_o +a_1x +a_2x^2 +...+a_nx^n`

`G(x) = \sum \limits ^(n)_(k=0) \ a_k x^k`

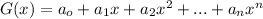
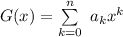
For the sequence above;

`G(x) = \sum \limits ^(29)_(k =0 ) (^(29)_(k)) x^k`

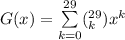
By applying binomial series
`(1+x)^n = \sum \limits ^n_(k=0) ( ^n_k) x^k`

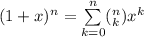
Thus:

`\mathbf{G(x) = (1 + x)^(29)}`