Answer:
1) k = -3
2) B. The curve would be narrower, but the vertex would be in the same position.
Explanation:
Transformations
For a > 0
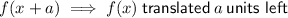

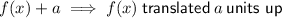

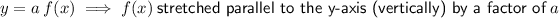

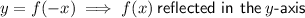
Question 1
When a graph is shifted up or down we add or subtract the number of units it has shifted from the function.
From inspection of the graph, the vertex of function j(x) is (0, 2)
From inspection of the graph, the vertex of function j(x) + k is (0, -1)
Therefore, function j(x) has been translated 3 units down.
Therefore, the value of k is -3, since the function of the graph is j(x) -3
Question 2
When discussing the stretching of curves, it is usual to always refer to it as a "stretch" rather than a stretch or compression.
If the scale factor a is 0 < a < 1 then the graph gets wider.
If the scale factor a is a > 1 then the graph gets narrower (i.e. "compressed").
h(x) to h(2x) means that the function h(x) has been stretched horizontally by a factor of 1/2. The other way to say this is that is have been compressed horizontally by a factor of 2. In any case, as a > 1 the graph gets narrower.
Therefore, the vertex would stay in the same place but the curve would be narrower.