Answer:
The value is

Step-by-step explanation:
From the question we are told that
The mass of the object is
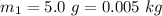
The net charge is
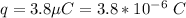
The mass of the second object is
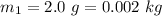
Generally for the first object the potential energy gained at the end of its acceleration is equal to its kinetic energy
i.e
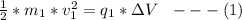
Here
 is the velocity of the first object
is the velocity of the first object
 is the potential difference through which it is accelerated
is the potential difference through which it is accelerated
Generally for the second object the potential energy gained at the end of its acceleration is equal to its kinetic energy
i.e

Here
 is the velocity of the second object and from the question it is
is the velocity of the second object and from the question it is

 is the potential difference through which it is accelerated
is the potential difference through which it is accelerated
So
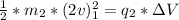
=>
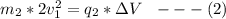
Generally dividing equation 2 by equation 1
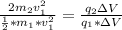
=>
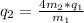
=>
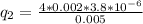
=>

=>
