Question

If 27.3% of a sample of silver-112 decays in 1.52 hours, what is the half-life (in hours to 3 decimal places)?

Answer 1

Answer: The half life of the sample of silver-112 is 3.303 hours.

Step-by-step explanation:

All radioactive decay processes undergoes first order reaction.

To calculate the rate constant for first order reaction, we use the integrated rate law equation for first order, which is:

`k=(2.303)/(t)\log ([A_o])/([A])`

where,

k = rate constant = ?

t = time taken = 1.52 hrs

`[A_o]` = Initial concentration of reactant = 100 g

[A] = Concentration of reactant left after time 't' = [100 - 27.3] = 72.7 g

Putting values in above equation, we get:

`k=(2.303)/(1.52hrs)\log (100)/(72.7)\\\\k= 0.2098hr^(-1)`

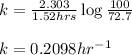
To calculate the half life period of first order reaction, we use the equation:

`t_(1/2)=(0.693)/(k)`

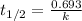
where,

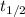`t_(1/2)` = half life period of first order reaction = ?

k = rate constant =
`0.2098hr^(-1)`

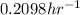
Putting values in above equation, we get:

`t_(1/2)=(0.693)/(0.2098hr^(-1))\\\\t_(1/2)=3.303hrs`

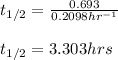
Hence, the half life of the sample of silver-112 is 3.303 hours.