Question

Suppose that a one-tail t - test is being applied to find out if the population mean is less than 100. The level of significance is 0.05 and 25 observations were sampled. The rejection region is:______

Answer 1

Reject H₀ if:
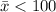`\bar x<100` or
`t_(calc.)<t_(0.05, 24)`.

Explanation:

The hypothesis for the one-tail t-test is:

H₀: The population mean is 100, i.e. μ = 100.

Hₐ: The population mean is less than 100, i.e. μ < 100.

The significance level of the test is, α = 0.05.

The number of observations in the sample is, n = 25.

The degrees of freedom of the test is:

df = n - 1

= 25 - 1

= 24

Compute the critical value of t as follows:

`t_(\alpha, (n-1))=t_(0.05, 24)=1.711`

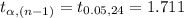
*Use a t-table.

The rejection region can be defined as follows:

Reject H₀ if:
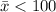`\bar x<100` or
`t_(calc.)<t_(0.05, 24)`.