Answer:
The disk covers a rotation of 90º after 3 seconds.
Step-by-step explanation:
Since the disk rotates at constant angular speed, we can determine the change in angular position (
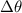 ), measured in sexagesimal degrees, by the following kinematic formula:
), measured in sexagesimal degrees, by the following kinematic formula:
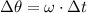 (1)
(1)
Where:
 - Angular velocity, measured in sexagesimal degrees per second.
- Angular velocity, measured in sexagesimal degrees per second.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
 and
and
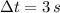 , then the change in angular position is:
, then the change in angular position is:
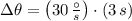
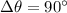
The disk covers a rotation of 90º after 3 seconds.