Answer:
The frequency of the second harmonic (
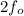 ) is 11.97 Hz.
) is 11.97 Hz.
Step-by-step explanation:
Given;
mass of the string, m = 25 g = 0.025kg
tension on the string, T = 43 N
length of the string, L = 12 m
The speed of wave on the string is given as;
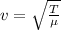
where;
μ is mass per unit length = 0.025 / 12 = 0.002083 kg/m
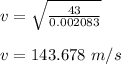
The wavelength of the first harmonic wave is given as;

The frequency of the first harmonic is given as;
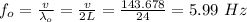
The wavelength of the second harmonic wave is given as;
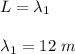
The frequency of the second harmonic is given as;
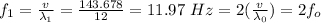
Therefore, the frequency of the second harmonic (
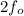 ) is 11.97 Hz.
) is 11.97 Hz.