Question

A pitot tube, mounted on an airplane flying at 8000 m standard altitude, reads a stagnation pressure of 52.2 kPa. Estimate (a) the velocity in mi/h and (b) the Mach number.

Answer 1

`524.31\ \text{mi/h}`

`0.761`

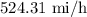
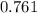
Step-by-step explanation:

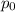`p_0` = Stagnation pressure = 52.2 kPa

`p` = Atmospheric pressure at 8000 m = 35.581 kPa (from chart)

M = Mach number

`v_s` = Velocity of sound at 8000 m = 308 m/s

v = Velocity of airplane

We have the following equation

`(p_0)/(p)=(1+0.2M^2)^(3.5)\\\Rightarrow M=\sqrt{(1)/(0.2)[((p_0)/(p))^{(1)/(3.5)}-1]}\\\Rightarrow M=\sqrt{(1)/(0.2)[((52.2)/(35.581))^{(1)/(3.5)}-1]}\\\Rightarrow M=0.761`

Mach number is given by

`M=(v)/(v_s)\\\Rightarrow v=Mv_s\\\Rightarrow v=0.761* 308\\\Rightarrow v=234.388\ \text{m/s}* (3600)/(1609.34)=524.31\ \text{mi/h}`

The velocity of the airplance is
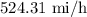`524.31\ \text{mi/h}` and has a mach number of
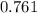`0.761`.