Question

A horizontal spring has a spring constant of 2.00 N/m. One end of the spring is attached to a fixed wall. A mass of 0.200 kilograms is attached to the free end of the spring and the spring is compressed by 0.500 meters from its natural length. The mass is released. What is the speed of the mass when the spring returns to its natural length?

a. 2.24 m/s
b. 2.50 m/s
c. 5.00 m/s
d. 1.58 m/s

Answer 1

(D) the speed of the mass when the spring returns to its natural length is 1.58 m/s.

Step-by-step explanation:

Given;

spring constant of the spring, k = 2 N/m

mass attached to the spring, m = 0.2 kg

compression of the spring, x = 0.5 m

Apply the principle of conservation of mechanical energy;

K.E = P.E

¹/₂m(v² - u²) = ¹/₂kx²

where;

u is the initial speed of the mass = 0

¹/₂mv² = ¹/₂kx²

mv² = kx²

`v^2= (kx^2)/(m) \\\\v= \sqrt{(kx^2)/(m)} \\\\v = \sqrt{((2)(0.5)^2)/(0.2)} \\\\v = 1.58 \ m/s`

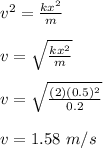
Therefore, the speed of the mass when the spring returns to its natural length is 1.58 m/s.