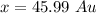Answer:
The value is
Step-by-step explanation:
From the question we are told that
The period of the asteroid is

Generally the average distance of the asteroid from the sun is mathematically represented as
![R = \sqrt[3]{ (G M * T^2 )/(4 \pi) }](https://img.qammunity.org/2021/formulas/physics/high-school/awrbrs2lamzily0nu2sjoonar5ggrfkm6m.png)
Here M is the mass of the sun with a value

G is the gravitational constant with value

![R = \sqrt[3]{ (6.67 *10^(-11) * 1.99*10^(30) * [5.55 *10^(9)]^2 )/(4 * 3.142 ) }](https://img.qammunity.org/2021/formulas/physics/high-school/23khmz6yerx1411d43obrfh4oqlx1w2zh4.png)
=>
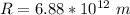
Generally
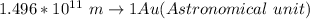
So
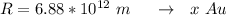
=>
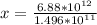
=>