Answer:
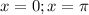
Explanation:
Let's first convert that
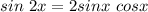 using the double angle formula.
using the double angle formula.
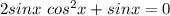
Now, if
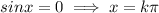 with
with
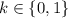 we get
we get
 which is indeed true, so we have a solution. Else, we can divide by
which is indeed true, so we have a solution. Else, we can divide by
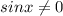 to get
to get
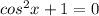 which has no real solutions (I like to think about it as the sum of two positive numbers, which is never zero).
which has no real solutions (I like to think about it as the sum of two positive numbers, which is never zero).