Answer:
The effect of doubling the diameter is increased the area to paint as 4 times. So, paint needed is 4 times than it was before. And the area is increased by 9 times when the diameter is increased by a factor of 3. So, paint needed is 9 times than before.
Explanation:
Please remember the concept
If side lengths are in the ratio a : b
Then the area are in the ratio of a^2 :b^2
The volume are in the ratio of a^3 :b^3,
When diameter is doubled, the area ratio becomes
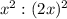 which is simplified to
which is simplified to
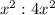
So, the area is increased by 4 times.
According to this concept , the diameter is increased by the scale factor 3.
Let the diameter of tank is 'x', so the diameter becomes "3x"
So, it's area ratio would be
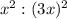
If we simplify it we get
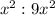
We conclude that area to be increased by 9 times.