Question

-

RO
SEROANATENG
BADA. SIMON
VVUIS
SEKOLAH MENENG
KERTAS
MATIK TINGKATAN 4
GIAN A. Jawab semua soalan
Fungsi kuadratik f(x) = x2 - 6x + c melalui titik B(-2,4). Apakah nilai bagi c?
The quadratic function f(x) = x2 - 6x + c passes through point B(-2,4). What is the
value of c?
A -12
B -6
C 6
D 12​

Answer 1

Given:

Quadratic function is

`f(x)=x^2-6x+c`

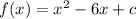
It passes through B(-2,4).

To find:

The value of c.

Solution:

The quadratic function passes through B(-2,4), it means the equation of quadratic equation must be true for the point B(-2,4).

We have,

`f(x)=x^2-6x+c`

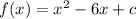
Putting x=-2 and f(x)=4, we get

`4=(-2)^2-6(-2)+c`

`4=4+12+c`

`4=16+c`

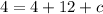
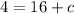
Subtract both sides by -16.

`4-16=c`

`-12=c`

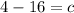
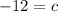
The value of c is -12.

Therefore, the correct option is A.