Question

M is directly proportional to r^3

When r = 4, M= 160
b) work out the value of r when m = 540

Answer 1

r=6

Explanation:

Proportions

We know M is directly proportional to
`r^3`

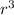
This can be written as

`M=kr^3`

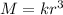
Where k is the constant of proportionality which will be determined knowing that when r = 4, M= 160. Substituting in the equation above:

`160=k\cdot 4^3`

`160=k\cdot 64`

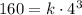
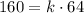
Solving for k:

`k=(160)/(64)=2.5`

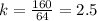
The equation is:

`M=2.5\cdot r^3`

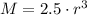
Now find r when M=540:

`540=2.5\cdot r^3`

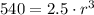
Dividing by 2.5:

`216=r^3`

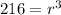
Taking cube roots:

`r=\sqrt[3]{216}`

r=6