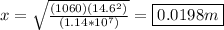Question

3

012 10.0 points
A car with mass 1060 kg crashes into a wall.
The car's velocity immediately before the col-
lision was 14.6 m/s and the bumper is com-
pressed like a spring with spring constant
1.14 × 107 N/m.
What is the maximum deformation of the
bumper for this collision?
Answer in units of m.
013 10

Answer 1

Hi there!

The maximum deformation of the bumper will occur when the car is temporarily at rest after the collision. We can use the work-energy theorem to solve.

Initially, we only have kinetic energy:

`KE = (1)/(2)mv^2`

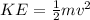
KE = Kinetic Energy (J)
m = mass (1060 kg)
v = velocity (14.6 m/s)

Once the car is at rest and the bumper is deformed to the maximum, we only have spring-potential energy:

`U_s = (1)/(2)kx^2`

k = Spring Constant (1.14 × 10⁷ N/m)

x = compressed distance of bumper (? m)

Since energy is conserved:

`E_I = E_f\\\\KE = U_s\\\\(1)/(2)mv^2 = (1)/(2)kx^2`

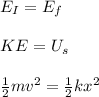
We can simplify and solve for 'x'.

`mv^2 = kx^2\\\\x = \sqrt{(mv^2)/(k)}`

Plug in the givens and solve.

`x = \sqrt{((1060)(14.6^2))/((1.14*10^7))} = \boxed{0.0198 m}`