Answer:
The dimensions of the smallest piece that can be used are: 10 by 20 and the area is 200 square inches
Explanation:
We have that:
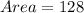
Let the dimension of the paper be x and y;
Such that:
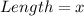
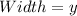
So:
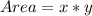
Substitute 128 for Area
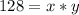
Make x the subject

When 1 inch margin is at top and bottom
The length becomes:
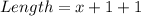
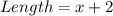
When 2 inch margin is at both sides
The width becomes:
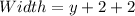
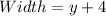
The New Area (A) is then calculated as:
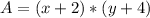
Substitute
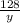 for x
for x
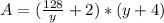
Open Brackets

Collect Like Terms
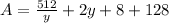
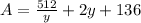
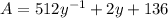
To calculate the smallest possible value of y, we have to apply calculus.
Different A with respect to y

Set
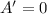
This gives:
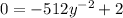
Collect Like Terms
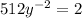
Multiply through by
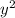
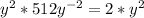
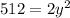
Divide through by 2
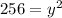
Take square roots of both sides
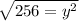
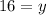
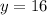
Recall that:

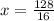
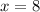
Recall that the new dimensions are:
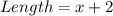
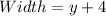
So:
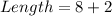
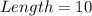
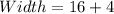

To double-check;
Differentiate A'


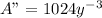
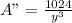
The above value is:
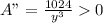
This means that the calculated values are at minimum.
Hence, the dimensions of the smallest piece that can be used are: 10 by 20 and the area is 200 square inches