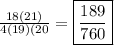Sum of 1/(123) + 1/(234) +....+1/(181920)

Question

asked Sep 2, 2023 133k views

1 Answer

Cafer Mert Ceyhan · Answer 1 · 2023-09-06T20:57:45+0000

Answer: 189/760

Explanation:

The series can be represented in sigma notation as:

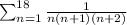
$\sum^(18)_(n=1) (1)/(n(n+1)(n+2))$

We can perform partial fraction decomposition as follows:

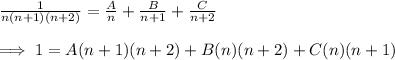
$(1)/(n(n+1)(n+2))=(A)/(n)+(B)/(n+1)+(C)/(n+2)\\\\ \implies 1=A(n+1)(n+2)+B(n)(n+2)+C(n)(n+1)$

If n = 0, then
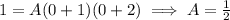
$1=A(0+1)(0+2) \implies A=(1)/(2)$

If n = -1, then
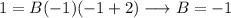
$1=B(-1)(-1+2) \longrightarrow B=-1$

If n = -2, then
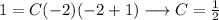
$1=C(-2)(-2+1) \longrightarrow C=(1)/(2)$

This means the series can be expressed as:

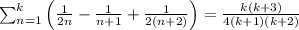
$\sum^(k)_(n=1) \left((1)/(2n)-(1)/(n+1)+(1)/(2(n+2)) \right)=(k(k+3))/(4(k+1)(k+2))$

Substituting in k=18,

$(18(21))/(4(19)(20)=\boxed{(189)/(760)}$