Question

Adult tickets for the game cost $6 each

and student tickets cost $3 each. A total of
1040 tickets worth $5400 were sold. How
many student tickets were sold?

Answer 1

280 student tickets were sold.

Explanation:

To solve this problem, we will have to create a system of equations. The first equation will represent the number of tickets sold.

Let
`a` = adult tickets.

Let
`s` = student tickets.

The first equation:

`a+s=1040`

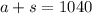
The second equation in our system will represent the total cost of the tickets sold:

`6a+3s=5400`

There are multiple ways to solve a system of equations, these include elimination, substitution, and graphing. Let's use the elimination method. By use of this method, I will distribute a
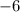`-6` into the first equation to eliminate the variable
`a`, to solve for
`s:`

`-6(a+s=1040)`

`6a+3s=5400`

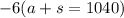
Distribute the
`-6`:

`-6a-6s=-6240`

`6a+3s=5400`

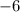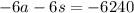
Combine the two equations:

`-3s=-840`

Divide both sides of the equation by the coefficient of
`s`, which is
`-3`:

`s=280`

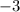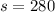
Therefore, 280 student tickets were sold.

-

Though we have our answer at this point in the problem, let's find how many adult tickets there are so we can substitute in our solved values to check our work & solution.

Substitute
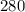`280` into the first initial equation:

`a+280=1040`

Subtract
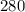`280` from both sides of the equation:

`a=760`

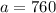
Therefore, 760 adult tickets were sold.

We now know that our numbers are correct because when added, they equal the number of tickets given in the problem:

`760+280=1040`

-

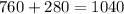
Now we've confirmed that information, but to be extra sure, we can substitute our solved values into the second equation in the system to make sure our numbers add up to the $5400 the tickets were worth:

`6(760)+3(280)=5400`

`4560+840=5400`

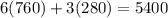
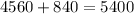
Now we know that all of our answers are correct!