Question

Hey! can someone give me a step-by-step explanation on how to solve this problem correctly? I know for a fact that I did it incorrectly.

Answer 1

Perhaps the 3 from the radius was squared to 9, and then multiplied by the 2 from the height to get 18 in the “1:18”
This is just a guess in case no one else answers your question you can try this

Answer 2

B. 1:18

Explanation Down Below

Explanation:

Hello!

First, let's find the volume of each cylinder by plugging in the given values.

Volume of a Cylinder:
`V = \pi r^2h`

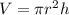
Cylinder A

Since the variables are the same as given in the formula, we can just use the formula as the volume.

`\implies{\boxed{{V = \pi r^2h}}`

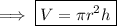
Cylinder B

We have to plug in 3r for the radius, and 2h for the height.

• 
  `V = \pi r^2 h`
• 
  `V = \pi (3r)^2(2h)`
• 
  `V = \pi(9r^2)(2h)`
• 
  `V = 18\pi r^2h`

`\implies \boxed{ V = 18\pi r^2h}`

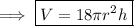
Ratio

We can see that the Volume of Cylinder B is just 18 times the Volume of Cylinder A, but we can find the same ratio using equations.

• 
  `\text{Ratio} = A:B`
• 
  `\text{Ratio} = \pi r^2h: 18\pi r^2h`
• 
  `\text{Ratio} = (\pi r^2h)/(18\pi r^2h)`
• 
  `\text{Ratio} = \frac{\\ot{\pi}\\ot {r^2}\\ot{h}}{18\\ot{\pi}\\ot{r^2}\\ot{h}}`
• 
  `\text{Ratio} = \frac1{18}`
• 
  `\text{Ratio} =1:18`

The answer is Option B. 1:18.