Rewrite the expression with a rational exponent as a radical expression.

Question

asked Oct 8, 2021 134k views

1 Answer

Timbl · Answer 1 · 2021-10-14T13:32:05+0000

Answer:

Rewriting the expression
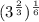(3^(2)/(3))^(1)/(6) with a rational exponent as a radical expression we get
$\mathbf{\sqrt[9]{3} }$

Explanation:

We need to rewrite the expression
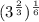(3^(2)/(3))^(1)/(6) with a rational exponent as a radical expression.

The expression given is:

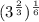
(3^(2)/(3))^(1)/(6)

First we will simply the expression using exponent rule
(a^m)^n=a^(mn)

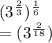
$(3^(2)/(3))^(1)/(6)\\=(3^(2)/(18))$

As we know 2 and 18 are both divisible by 2, we can write

=(3^(1)/(9))

Now we know that
$a^(1)/(9)=\sqrt[9]{a}$

Using this we get

$=\sqrt[9]{3}$

So, rewriting the expression
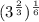(3^(2)/(3))^(1)/(6) with a rational exponent as a radical expression we get
$\mathbf{\sqrt[9]{3} }$