Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of a second.

f(x) = -16x^2+272x+110

Answer 1

The time that the rocket will hit the ground will be:

• x = 17.40 seconds

Explanation:

Given the expression

`f\left(x\right)\:=-16x^2+272x+110`

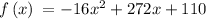
Here:

• x represents the time in seconds

• y represents the height of the rocket

We know that when the rocket will hit the ground, the height will get y = 0

i.e.

`0\:=-16x^2+272x+110`

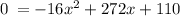
solving for x to determine the time that the rocket takes when it will hit the ground.

so

`-16x^2+272x+110=0`

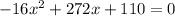
subtract 110 from both sides

`-16x^2+272x+110-110=0-110`

`-16x^2+272x=-110`

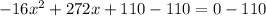
Divide both sides by -16

`(-16x^2+272x)/(-16)=(-110)/(-16)`

`x^2-17x=(55)/(8)`

`\mathrm{Add\:}\left(-(17)/(2)\right)^2\mathrm{\:to\:both\:sides}`

`x^2-17x+\left(-(17)/(2)\right)^2=(55)/(8)+\left(-(17)/(2)\right)^2`

`x^2-17x+\left(-(17)/(2)\right)^2=(633)/(8)`

`\left(x-(17)/(2)\right)^2=(633)/(8)`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

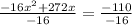
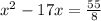
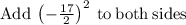
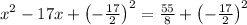
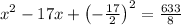
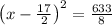
solving

`x-(17)/(2)=\sqrt{(633)/(8)}`

`x=(√(1266))/(4)+(17)/(2)`

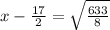
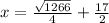
x = 17.40 seconds

also solving

`x-(17)/(2)=-\sqrt{(633)/(8)}`

`x=-(√(1266))/(4)+(17)/(2)`

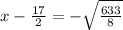
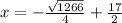
x = -0.40 seconds

As time can not be negative.

Thus, the value of x = 17.40 seconds

Therefore, the time that the rocket will hit the ground will be:

• x = 17.40 seconds